Next: Serie di Taylor Up: Aspetti matematici Previous: Le leggi di Fick Indice

Integrazione numerica

Per simulare la diffusione mediante una sequenza di passi discreti bisogna applicare all' equazione differenziale (

) un opportuno schema di integrazione numerica. In generale si hanno due tipologie di integrazione numerica:

schema di integrazione esplicito;
schema di integrazione implicito.

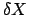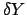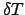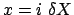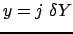Per poter discretizzare la funzione di diffusione si divide sia l' area in esame, sia il tempo, in intervalli della stessa lunghezza. Siano $\delta X$ e $\delta Y$ i passi di integrazione spaziale e $\delta T$ il passo di integrazione temporale. Abbiamo costruito così una griglia che copre tutto lo spazio per ciascun passo temporale. 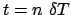Esprimiamo le coordinate in questo modo: $x = i\ \delta X$ , $y = j\ \delta Y$ e $t = n\ \delta T$ con i, j, n numeri naturali. 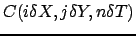In questo modo si può indicare il valore della concentrazione in ciascun punto della griglia come $C(i\delta X, j\delta Y, n\delta T)$ che per semplicità scriveremo $C_{i,j,n}$ .

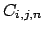**Figura:** discretizzazione del dominio

Subsections

2006-02-17