



Next: Condizioni iniziali e al
Up: Integrazione numerica
Previous: Metodo esplicito
Indice
Un metodo alternativo, molto usato, fu proposto da Crank e Nicolson
nel 1947. Questo metodo, descritto in ``Numerical solution of
partial differential equations'' di Smith [11], consiste
nel sostituire
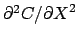 con la media delle
differenze finite (
con la media delle
differenze finite (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) al tempo n-esimo e (n+1)-esimo,
) al tempo n-esimo e (n+1)-esimo,
Nello stesso modo si ricava la media per quanto riguarda la variabile
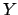
Combinando la legge di Fick (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) e la (
) e la (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
inserendo la media delle differenze finite per le variabili
)
inserendo la media delle differenze finite per le variabili 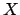 e
e
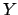 si ottiene:
si ottiene:
Sostituendo nella (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) la (
) la (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) e la (
) e la (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
si ottiene:
)
si ottiene:
Infine, ponendo
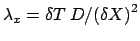 e
e
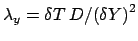 e separando la concentrazione dell'
istante
e separando la concentrazione dell'
istante 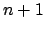 dall' istante
dall' istante 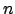 , si ottiene l' equazione
, si ottiene l' equazione
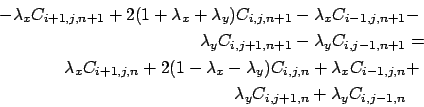 |
(2.13) |
che esprime la concentrazione nel tempo 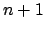 della cella
della cella
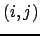 -esima e delle sue adiacenti in funzione dello stato che hanno
le celle nell' istante precedente.
-esima e delle sue adiacenti in funzione dello stato che hanno
le celle nell' istante precedente.
Se 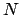 è il numero di tasselli spaziali lungo l' asse
è il numero di tasselli spaziali lungo l' asse 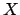 ed
ed
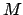 il numero di tasselli spaziali lungo l' asse
il numero di tasselli spaziali lungo l' asse 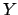 allora
allora
![$ i\in
[0,N-1]$](img64.png) e
e
![$ j \in [0,M-1]$](img65.png) . Il metodo
. Il metodo
di Crank-Nicolson richiede la
soluzione simultanea di
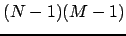 equazioni algebriche per ogni passo
temporale
equazioni algebriche per ogni passo
temporale 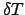 ; questo perché cinque valori incogniti
della concentrazione
; questo perché cinque valori incogniti
della concentrazione 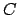 compaiono in ciascuna equazione. Per giungere
alla soluzione non si usano metodi di eliminazione diretta, ma il
sistema viene risolto iterativamente. Questo metodo, in cui le
soluzioni sono ottenute dalla risoluzione simultanea di equazioni
è chiamato ``metodo implicito''. Si può procedere con il metodo
di Crank-Nicolson usando sia intervalli temporali ampi che brevi.
compaiono in ciascuna equazione. Per giungere
alla soluzione non si usano metodi di eliminazione diretta, ma il
sistema viene risolto iterativamente. Questo metodo, in cui le
soluzioni sono ottenute dalla risoluzione simultanea di equazioni
è chiamato ``metodo implicito''. Si può procedere con il metodo
di Crank-Nicolson usando sia intervalli temporali ampi che brevi.




Next: Condizioni iniziali e al
Up: Integrazione numerica
Previous: Metodo esplicito
Indice
2006-02-17
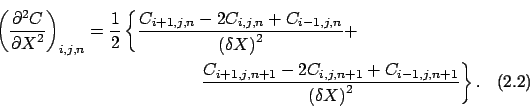
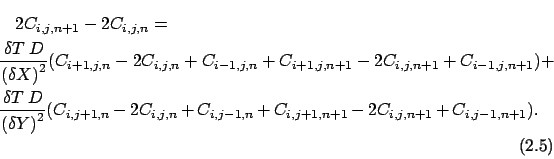
![]() è il numero di tasselli spaziali lungo l' asse
è il numero di tasselli spaziali lungo l' asse ![]() ed
ed
![]() il numero di tasselli spaziali lungo l' asse
il numero di tasselli spaziali lungo l' asse ![]() allora
allora
![]() e
e
![]() . Il metodo
. Il metodo
![]() equazioni algebriche per ogni passo
temporale
equazioni algebriche per ogni passo
temporale ![]() ; questo perché cinque valori incogniti
della concentrazione
; questo perché cinque valori incogniti
della concentrazione ![]() compaiono in ciascuna equazione. Per giungere
alla soluzione non si usano metodi di eliminazione diretta, ma il
sistema viene risolto iterativamente. Questo metodo, in cui le
soluzioni sono ottenute dalla risoluzione simultanea di equazioni
è chiamato ``metodo implicito''. Si può procedere con il metodo
di Crank-Nicolson usando sia intervalli temporali ampi che brevi.
compaiono in ciascuna equazione. Per giungere
alla soluzione non si usano metodi di eliminazione diretta, ma il
sistema viene risolto iterativamente. Questo metodo, in cui le
soluzioni sono ottenute dalla risoluzione simultanea di equazioni
è chiamato ``metodo implicito''. Si può procedere con il metodo
di Crank-Nicolson usando sia intervalli temporali ampi che brevi.