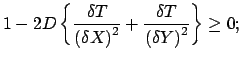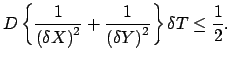Next: Metodo implicito di Crank-Nicolson
Up: Integrazione numerica
Previous: Serie di Taylor
Indice
Si considera la regione in esame coperta da una griglia
tridimensionale, Figura ![[*]](file:/usr/share/latex2html/icons/crossref.png) , si può usare la serie di
Taylor (
, si può usare la serie di
Taylor (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) nella direzione
) nella direzione 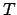 ponendo
ponendo 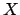 e
e 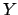 costanti:
costanti:
dalla (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) ne consegue che
) ne consegue che
Il termine
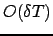 significa che i termini omessi sono dell'
ordine di
significa che i termini omessi sono dell'
ordine di 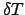 . Similmente si applica la serie di Taylor
(
. Similmente si applica la serie di Taylor
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) nella direzione
) nella direzione 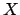 considerando
considerando 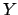 e
e 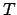 costanti
costanti
sommando la (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) e la
) e la ![[*]](file:/usr/share/latex2html/icons/crossref.png) ricaviamo
ricaviamo
Analogamente, integrando lungo l' asse 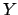 si ottiene
si ottiene
Sostituendo la (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), (
), (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) e (
) e (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
nell' equazione della diffusione (
)
nell' equazione della diffusione (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) si ottiene la legge che ci
permette di calcolare la
) si ottiene la legge che ci
permette di calcolare la
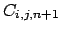 , cioè la concentrazione al
tempo
, cioè la concentrazione al
tempo
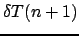 . Per fare ciò avremo necessariamente
bisogno dei valori della concentrazione di partenza (tempo
. Per fare ciò avremo necessariamente
bisogno dei valori della concentrazione di partenza (tempo 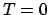 ) e
dei valori al contorno. L' equazione ottenuta con lo schema di
integrazione esplicito delle differenze finite è la seguente
) e
dei valori al contorno. L' equazione ottenuta con lo schema di
integrazione esplicito delle differenze finite è la seguente
Questo metodo è computazionalmente molto efficiente; di contro la
condizione di stabilità è molto severa perché impone l' uso
di 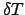 molto piccoli. La restrizione di stabilità si
trova ponendo il coefficiente di
molto piccoli. La restrizione di stabilità si
trova ponendo il coefficiente di 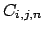 maggiore o uguale a
zero:
maggiore o uguale a
zero:
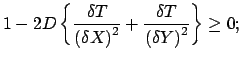 |
|
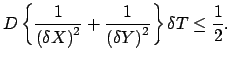 |
(2.12) |




Next: Metodo implicito di Crank-Nicolson
Up: Integrazione numerica
Previous: Serie di Taylor
Indice
2006-02-17
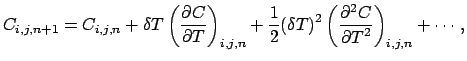
![]() ), (
), (![]() ) e (
) e (![]() )
nell' equazione della diffusione (
)
nell' equazione della diffusione (![]() ) si ottiene la legge che ci
permette di calcolare la
) si ottiene la legge che ci
permette di calcolare la
![]() , cioè la concentrazione al
tempo
, cioè la concentrazione al
tempo
![]() . Per fare ciò avremo necessariamente
bisogno dei valori della concentrazione di partenza (tempo
. Per fare ciò avremo necessariamente
bisogno dei valori della concentrazione di partenza (tempo ![]() ) e
dei valori al contorno. L' equazione ottenuta con lo schema di
integrazione esplicito delle differenze finite è la seguente
) e
dei valori al contorno. L' equazione ottenuta con lo schema di
integrazione esplicito delle differenze finite è la seguente