



Next: Metodo esplicito
Up: Integrazione numerica
Previous: Integrazione numerica
Indice
Sia 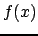 una funzione reale definita in un intervallo
una funzione reale definita in un intervallo
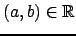 e sia
e sia
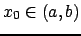 si vuole costruire, se possibile,
un polinomio
si vuole costruire, se possibile,
un polinomio 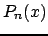 di grado
di grado 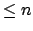 che abbia in
che abbia in 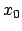 il medesimo
comportamento della
il medesimo
comportamento della 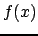 , nel senso che, posto
, nel senso che, posto
risulti
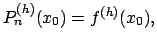 con
con 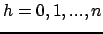 .
Derivando il polinomio nel punto
.
Derivando il polinomio nel punto 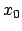 tutti gli addendi dopo il primo
si annullano e risulta
tutti gli addendi dopo il primo
si annullano e risulta
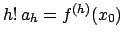 per ogni
per ogni
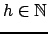 . Ne segue necessariamente che
. Ne segue necessariamente che
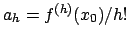 ,
sostituendo la formula nella (
,
sostituendo la formula nella (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) si ottiene
) si ottiene
La condizione necessaria e sufficiente affinché aumentando 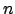 la
formula (
la
formula (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) approssimi meglio la funzione
) approssimi meglio la funzione 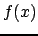 è che
è che
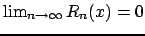 . Si ottiene
così la cosiddetta serie di Taylor [10]
. Si ottiene
così la cosiddetta serie di Taylor [10]
2006-02-17
![]() la
formula (
la
formula (![]() ) approssimi meglio la funzione
) approssimi meglio la funzione ![]() è che
è che
![]() . Si ottiene
così la cosiddetta serie di Taylor [10]
. Si ottiene
così la cosiddetta serie di Taylor [10]