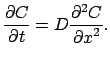Next: Integrazione numerica
Up: Aspetti matematici
Previous: Aspetti matematici
Indice
La seconda legge di Fick descrive il processo di diffusione di un
fluido immerso in un ambiente. L' equazione della diffusione è
Essa descrive la variazione nel tempo della concentrazione 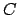 del
fluido. La variazione di concentrazione è funzione del tempo e
dello spazio;
del
fluido. La variazione di concentrazione è funzione del tempo e
dello spazio; 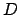 è il coefficiente di diffusione; dipende
strettamente dall' ambiente in cui è immerso il fluido e indica
la rapidità di propagazione. La legge (
è il coefficiente di diffusione; dipende
strettamente dall' ambiente in cui è immerso il fluido e indica
la rapidità di propagazione. La legge (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) riguarda lo
spostamento nella sola direzione
) riguarda lo
spostamento nella sola direzione 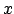 ; nel caso di diffusione
bidimensionale, l' equazione da utilizzare è invece della forma:
; nel caso di diffusione
bidimensionale, l' equazione da utilizzare è invece della forma:
L' espressione (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) considera una regione piana
rettangolare. In questo caso la funzione
) considera una regione piana
rettangolare. In questo caso la funzione 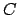 dipenderà da tre
variabili,
dipenderà da tre
variabili, 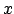 e
e 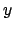 per quanto riguarda lo spazio e
per quanto riguarda lo spazio e 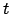 per il
tempo.
per il
tempo.
2006-02-17