Un sistema lineare può essere espresso come un' equazione
sotto forma matriciale. Si considera il seguente sistema lineare in ![]() incognite
incognite
![]()
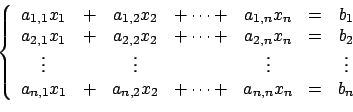
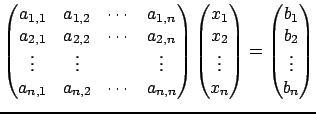
Senza la perdita di informazioni possiamo trasformare la funzione a
tre incognite ![]() in una a due incognite. La trasformazione parte dal
presupposto che si può utilizzare un solo indice
in una a due incognite. La trasformazione parte dal
presupposto che si può utilizzare un solo indice ![]() in luogo di
in luogo di ![]() e
e ![]() , per identificare lo spazio.
, per identificare lo spazio. ![]() si ottiene in questo modo:
si ottiene in questo modo:
![]() . L' equazione della diffusione integrata (
. L' equazione della diffusione integrata (![]() )
ora assume la forma
)
ora assume la forma
Per poter scrivere equazione (![]() ) nella forma del sistema
(
) nella forma del sistema
(![]() ) introduciamo la matrice
) introduciamo la matrice ![]() .
.
La matrice ![]() è una matrice sparsa. I suoi elementi sono per la
maggior parte uguali a zero, ed ha al più cinque elementi diversi
da zero per ogni riga. Per comprendere la sua struttura dividiamo
è una matrice sparsa. I suoi elementi sono per la
maggior parte uguali a zero, ed ha al più cinque elementi diversi
da zero per ogni riga. Per comprendere la sua struttura dividiamo ![]() in sottomatrici. Siano
in sottomatrici. Siano ![]() e
e ![]() due matrici di dimensioni
due matrici di dimensioni
![]()
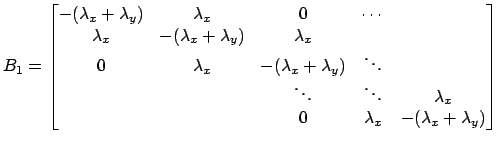

Ponendo
![]() , il vettore delle incognite
, il vettore delle incognite ![]() corrisponderà al vettore della concentrazione
corrisponderà al vettore della concentrazione ![]() e
sostituendo a
e
sostituendo a ![]() la seguente espressione
la seguente espressione
![]() , il
sistema
, il
sistema ![]() diviene
diviene