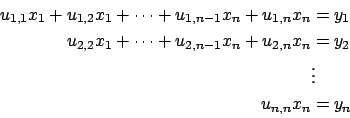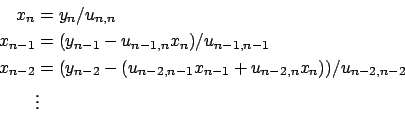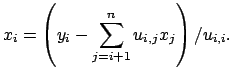Next: Esistenza delle soluzioni e
Up: Metodo di eliminazione di
Previous: Fattorizzazione LU
Indice
Sostituzione in avanti e a ritroso
La sostituzione in avanti risolve il sistema (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) in tempo
) in tempo
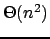 . Si può scrivere l' eq. (
. Si può scrivere l' eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) come
) come
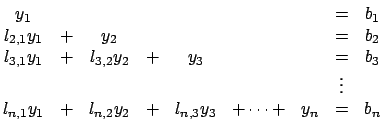 |
(2.21) |
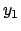 si trova direttamente dalla prima equazione del sistema,
una volta trovato
si trova direttamente dalla prima equazione del sistema,
una volta trovato 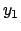 si sostituisce nella seconda equazione
ottenendo
si sostituisce nella seconda equazione
ottenendo 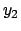 . In generale, sostituendo
. In generale, sostituendo
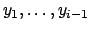 in
avanti nella
in
avanti nella 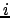 -esima equazione si trova
-esima equazione si trova 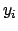 .
.
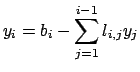 |
(2.22) |
La sostituzione a ritroso è analoga alla sostituzione in
avanti, con l' unica differenza che viene risolta prima l' 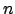 -esima
equazione, poi si opera a ritroso fino alla prima equazione. Questo
metodo serve per risolvere le equazioni di tipo
(
-esima
equazione, poi si opera a ritroso fino alla prima equazione. Questo
metodo serve per risolvere le equazioni di tipo
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ). Riscrivendo il sistema come
). Riscrivendo il sistema come
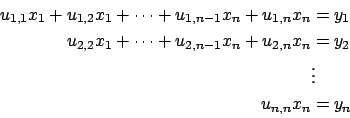 |
(2.23) |
si possono calcolare
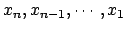 una dopo l' altra
come segue:
una dopo l' altra
come segue:
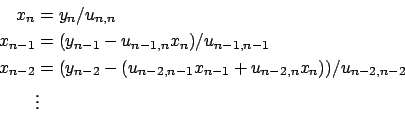 |
(2.24) |
La formula generale è la seguente:
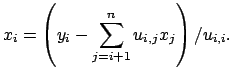 |
(2.25) |
Entrambi i metodi, implicito e esplicito, vengono implementati nella
funzione LUsolve() spiegata nel paragrafo ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.




Next: Esistenza delle soluzioni e
Up: Metodo di eliminazione di
Previous: Fattorizzazione LU
Indice
2006-02-17
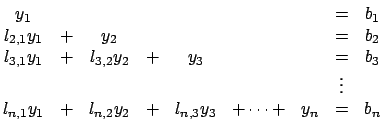
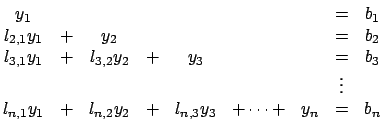
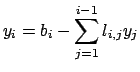
![]() -esima
equazione, poi si opera a ritroso fino alla prima equazione. Questo
metodo serve per risolvere le equazioni di tipo
(
-esima
equazione, poi si opera a ritroso fino alla prima equazione. Questo
metodo serve per risolvere le equazioni di tipo
(![]() ). Riscrivendo il sistema come
). Riscrivendo il sistema come