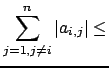Next: Il simulatore
Up: Aspetti matematici
Previous: Sostituzione in avanti e
Indice
Si è precedentemente ipotizzato che la matrice 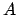 si possa
sempre scomporre in due matrici
si possa
sempre scomporre in due matrici 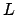 ed
ed 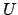 . Questo non è in generale
possibile per tutte le matrici. Mostreremo di seguito che la matrice
dei coefficienti
. Questo non è in generale
possibile per tutte le matrici. Mostreremo di seguito che la matrice
dei coefficienti 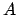 utilizzata nell' applicazione del metodo
implicito rispetta delle condizioni grazie alle quali
è possibile applicare il metodo di Gauss. I primi tre teoremi
presentati in questa sezione sono stati estratti dal testo `` Metodi numerici per l' algebra lineare'' di Bini, Capovani e
Menchi. Il teorema
utilizzata nell' applicazione del metodo
implicito rispetta delle condizioni grazie alle quali
è possibile applicare il metodo di Gauss. I primi tre teoremi
presentati in questa sezione sono stati estratti dal testo `` Metodi numerici per l' algebra lineare'' di Bini, Capovani e
Menchi. Il teorema ![[*]](file:/usr/share/latex2html/icons/crossref.png) ci garantisce che è i sistemi
ottenuti dalla fattorizzazione LU ammettono una soluzione.
ci garantisce che è i sistemi
ottenuti dalla fattorizzazione LU ammettono una soluzione.
Una matrice 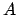 si dice non singolare se esiste
una matrice
si dice non singolare se esiste
una matrice 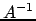 tale che
tale che
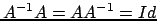 oppure
analogamente se il suo determinante è diverso
da zero (
oppure
analogamente se il suo determinante è diverso
da zero (
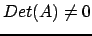 .) Data una matrice
.) Data una matrice
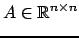 , una sottomatrice principale di
testa di ordine
, una sottomatrice principale di
testa di ordine 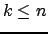 di
di 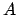 è una matrice
è una matrice
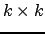 formata dagli elementi
formata dagli elementi 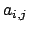 ,
,
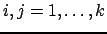 .
.
Teorema 2.5.1
Se 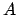 è una matrice a predominanza
diagonale stretta per righe, cioè vale che
allora
è una matrice a predominanza
diagonale stretta per righe, cioè vale che
allora 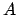 è non singolare.
è non singolare.
Dimostrazione.
[
Dimostrazione.] Se
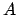
è a predominanza
diagonale in senso stretto allora, dal primo teorema di Gerschgorin
[
14], risulta che i cerchi di Gerschgorin (cerchi nel
piano complesso di centro centro
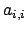
e raggio
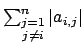
) avendo raggio
minore della distanza del centro dall' origine del piano complesso
non possono includere l' origine, quindi
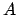
è non singolare.

Se 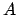 è una matrice a predominanza diagonale stretta lo saranno
anche tutte le sue sottomatrici principali di testa e quindi,
applicando il teorema precedente, saranno anch' esse non singolari.
è una matrice a predominanza diagonale stretta lo saranno
anche tutte le sue sottomatrici principali di testa e quindi,
applicando il teorema precedente, saranno anch' esse non singolari.
Teorema 2.5.2
Sia 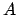 una matrice di ordine
una matrice di ordine 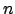 e siano
e siano 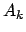 le sue
sottomatrici principali di testa di ordine
le sue
sottomatrici principali di testa di ordine 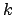 . Se
. Se 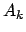 è non
singolare per
è non
singolare per
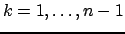 , allora esiste ed è unica la
fattorizzazione LU di
, allora esiste ed è unica la
fattorizzazione LU di 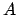 .
.
Dimostrazione.
[
Dimostrazione.]
Si procede per induzione. Se
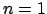
,
![$ A_1 = [a_{1,1}]$](img171.png)
e quindi si ha
![$ L = [1]$](img172.png)
e
![$ U = [a_{1,1}]$](img173.png)
, univocamente. Se
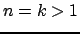
, la matrice
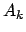
può essere partizionata nel modo seguente
In cui
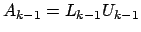
, con
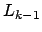
matrice triangolare
inferiore con elementi principali uguali ad
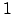
e
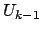
triangolare
superiore. Posto
occorre determinare
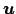
,
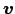
e
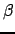
in
modo che
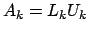
. Poiché risulta
si ha che la relazione
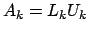
è verificata se e solo se
I vettori
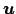
e
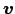
risultano determinati
univocamente dalle prime due relazioni, poiché
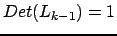
e
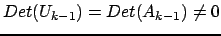
in quanto
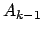
è
non singolare. Dalla terza relazione si ricava univocamente
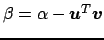
.

Teorema 2.5.3
Se esiste una fattorizzazione LU di 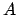 allora il metodo
di Gauss è applicabile.
allora il metodo
di Gauss è applicabile.
La nostra matrice 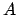 , che ricordiamo essere
, che ricordiamo essere
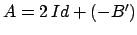 , ha
predominanza diagonale stretta, infatti
, ha
predominanza diagonale stretta, infatti
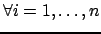 si ha
si ha
Teorema 2.5.4
Se A è fattorizzabile LU allora i sistemi Ly = b ed Ux =
y ammettono entrambi una soluzione.
Dimostrazione.
[
Dimostrazione.]
Sia
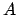
una matrice quadrata e siano
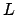
ed
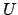
due matrici tali che
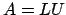
si ha che
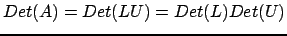
. Dato che
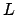
è triangolare inferiore unitaria il suo determinante è uno
(
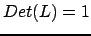
). Si ha quindi
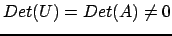
allora sia
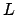
, sia
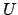
sono non singolari quindi i sistemi ammettono una
soluzione.





Next: Il simulatore
Up: Aspetti matematici
Previous: Sostituzione in avanti e
Indice
2006-02-17
![]() si dice non singolare se esiste
una matrice
si dice non singolare se esiste
una matrice ![]() tale che
tale che
![]() oppure
analogamente se il suo determinante è diverso
da zero (
oppure
analogamente se il suo determinante è diverso
da zero (
![]() .) Data una matrice
.) Data una matrice
![]() , una sottomatrice principale di
testa di ordine
, una sottomatrice principale di
testa di ordine ![]() di
di ![]() è una matrice
è una matrice
![]() formata dagli elementi
formata dagli elementi ![]() ,
,
![]() .
.
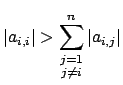
![]() è una matrice a predominanza diagonale stretta lo saranno
anche tutte le sue sottomatrici principali di testa e quindi,
applicando il teorema precedente, saranno anch' esse non singolari.
è una matrice a predominanza diagonale stretta lo saranno
anche tutte le sue sottomatrici principali di testa e quindi,
applicando il teorema precedente, saranno anch' esse non singolari.
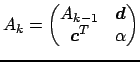
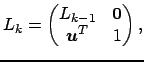
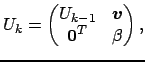
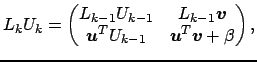
![]() , che ricordiamo essere
, che ricordiamo essere
![]() , ha
predominanza diagonale stretta, infatti
, ha
predominanza diagonale stretta, infatti
![]() si ha
si ha