



Next: Sostituzione in avanti e
Up: Metodo di eliminazione di
Previous: Metodo di eliminazione di
Indice
Fattorizzazione LU
Il processo di fattorizzazione consiste nel trovare una scomposizione
della matrice dei coefficienti 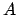 in due matrici
in due matrici 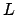 ed
ed 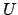 in modo
che sia
in modo
che sia 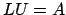 .
Per fare ciò si sottraggono i multipli della prima equazione del
sistema dalle altre equazioni così che la prima variabile sia
rimossa da quelle equazioni. Si sottraggono i multipli della
seconda equazione dalla terza e dalle successive così che la prima
e la seconda variabile siano rimosse. Si itera il procedimento
fino a quando la matrice non assume la forma triangolare superiore, si
arriva così alla matrice
.
Per fare ciò si sottraggono i multipli della prima equazione del
sistema dalle altre equazioni così che la prima variabile sia
rimossa da quelle equazioni. Si sottraggono i multipli della
seconda equazione dalla terza e dalle successive così che la prima
e la seconda variabile siano rimosse. Si itera il procedimento
fino a quando la matrice non assume la forma triangolare superiore, si
arriva così alla matrice 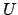 . La matrice
. La matrice 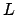 è composta da
moltiplicatori che causano l' eliminazione delle variabili.
L' algoritmo può essere facilmente descritto in modo induttivo
su
è composta da
moltiplicatori che causano l' eliminazione delle variabili.
L' algoritmo può essere facilmente descritto in modo induttivo
su 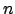 . Se
. Se 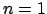 si sceglie
si sceglie 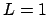 ed
ed
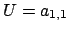 . Per
. Per 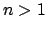 si
taglia
si
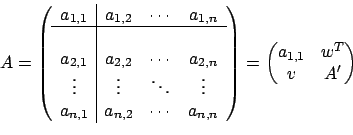
taglia 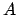 in quattro parti
dove
in quattro parti
dove 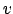 è un vettore colonna e
è un vettore colonna e 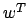 è un vettore riga,
entrambi di dimensione
è un vettore riga,
entrambi di dimensione 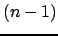 .
. 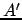 è una matrice
è una matrice
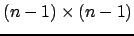 . È facile verificare che
. È facile verificare che 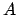 ammette la seguente
scomposizione
Si intende con
ammette la seguente
scomposizione
Si intende con
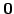 nella prima e nella seconda matrice,
rispettivamente, vettori riga e colonna di dimensione
nella prima e nella seconda matrice,
rispettivamente, vettori riga e colonna di dimensione 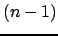 , che
hanno tutti gli elementi uguali a zero.
, che
hanno tutti gli elementi uguali a zero.
Supponendo vero questo metodo per la matrice
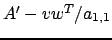 di
dimensioni
di
dimensioni
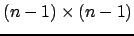 , si dimostra per
, si dimostra per 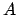 di dimensioni
di dimensioni
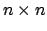 . Siano
. Siano 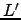 e
e 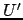 le matrici ottenute dalla
scomposizione della sottomatrice
le matrici ottenute dalla
scomposizione della sottomatrice
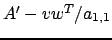 , si ha
, si ha
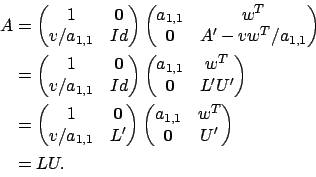 |
(2.20) |
Poiché 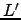 è triangolare inferiore unitaria, anche
è triangolare inferiore unitaria, anche 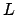 lo
è. Poiché
lo
è. Poiché 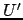 è triangolare superiore, anche
è triangolare superiore, anche 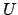 lo
è. Si ottiene così ottenuto una fattorizzazione LU per la
matrice
lo
è. Si ottiene così ottenuto una fattorizzazione LU per la
matrice 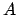 .
.
Osserviamo che se l' elemento 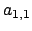 fosse uguale a zero questo
metodo non funzionerebbe, perché si dividerebbe per zero, non si
può applicare, inoltre, se l' elemento
fosse uguale a zero questo
metodo non funzionerebbe, perché si dividerebbe per zero, non si
può applicare, inoltre, se l' elemento 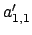 della matrice
della matrice
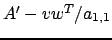 fosse zero e così via. In questi casi non è
possibile applicare la fattorizzazione LU. Vedremmo successivamente
che la la classe di matrici a cui verrà applicata la
fattorizzazione presenta delle caratteristiche che garantiscono che non
si verifichi mai questo inconveniente. Gli
elementi per cui si divide durante la fattorizzazione LU sono chiamati
perni. Vengono scelti come perni gli elementi sulla diagonale
perchè nel nostro caso sono i valori maggiori di ogni riga; essi
fanno si che gli errori di arrotondamento siano minori e di conseguenza
aumenti la stabilità.
fosse zero e così via. In questi casi non è
possibile applicare la fattorizzazione LU. Vedremmo successivamente
che la la classe di matrici a cui verrà applicata la
fattorizzazione presenta delle caratteristiche che garantiscono che non
si verifichi mai questo inconveniente. Gli
elementi per cui si divide durante la fattorizzazione LU sono chiamati
perni. Vengono scelti come perni gli elementi sulla diagonale
perchè nel nostro caso sono i valori maggiori di ogni riga; essi
fanno si che gli errori di arrotondamento siano minori e di conseguenza
aumenti la stabilità.
Il codice della fattorizzazione LU è riportato nel cap ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.




Next: Sostituzione in avanti e
Up: Metodo di eliminazione di
Previous: Metodo di eliminazione di
Indice
2006-02-17

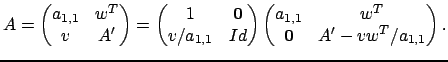
![]() di
dimensioni
di
dimensioni
![]() , si dimostra per
, si dimostra per ![]() di dimensioni
di dimensioni
![]() . Siano
. Siano ![]() e
e ![]() le matrici ottenute dalla
scomposizione della sottomatrice
le matrici ottenute dalla
scomposizione della sottomatrice
![]() , si ha
, si ha
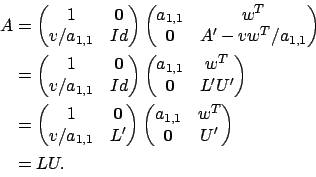
![]() fosse uguale a zero questo
metodo non funzionerebbe, perché si dividerebbe per zero, non si
può applicare, inoltre, se l' elemento
fosse uguale a zero questo
metodo non funzionerebbe, perché si dividerebbe per zero, non si
può applicare, inoltre, se l' elemento ![]() della matrice
della matrice
![]() fosse zero e così via. In questi casi non è
possibile applicare la fattorizzazione LU. Vedremmo successivamente
che la la classe di matrici a cui verrà applicata la
fattorizzazione presenta delle caratteristiche che garantiscono che non
si verifichi mai questo inconveniente. Gli
elementi per cui si divide durante la fattorizzazione LU sono chiamati
perni. Vengono scelti come perni gli elementi sulla diagonale
perchè nel nostro caso sono i valori maggiori di ogni riga; essi
fanno si che gli errori di arrotondamento siano minori e di conseguenza
aumenti la stabilità.
fosse zero e così via. In questi casi non è
possibile applicare la fattorizzazione LU. Vedremmo successivamente
che la la classe di matrici a cui verrà applicata la
fattorizzazione presenta delle caratteristiche che garantiscono che non
si verifichi mai questo inconveniente. Gli
elementi per cui si divide durante la fattorizzazione LU sono chiamati
perni. Vengono scelti come perni gli elementi sulla diagonale
perchè nel nostro caso sono i valori maggiori di ogni riga; essi
fanno si che gli errori di arrotondamento siano minori e di conseguenza
aumenti la stabilità.
![]() .
.