Coefficienti variabili

Nell' esempio precedente abbiamo considerato un caso in cui i coefficienti di diffusione restavano uguali ad uno in tutta l' area di studio. In generale il risultato di una simulazione risulta essere un buon modello se si avvicina il più possibile alla realtà. Nella maggior parte delle situazioni in cui si può osservare un fenomeno diffusivo la zona in osservazione difficilmente risulta uniforme. Esistono molti fattori che influiscono sul moto delle molecole come ad esempio la temperatura, la pressione, l' umidità, la densità, i campi magnetici, la luminosità...

Tutti questi fattori, che possono variare da un punto all' altro della zona sotto esame, vengono considerati nel coefficiente di diffusione. Nell' esempio seguente il fluido sarà tutto concentrato verso il centro, quello che varierà saranno i coefficienti di diffusione che andranno a formare un gradiente simmetrico (Figura ).

Figura: Coefficienti variabili

[concentrazione] [coefficienti di diffusione]

$ fick -x 4 -y 4 - -dt 2 test/ciambella.bmp test/grad_simm.bmp

[$t_0$] [$t_2$] [$t_4$] [$t_6$] [$t_8$] [$t_{10}$]

Figura: Variazione della concentrazione con coefficienti variabili

[$t_{12}$] [$t_{14}$] [$t_{16}$] [$t_{18}$] [$t_{20}$] [$t_{22}$]

Si nota chiaramente sia dall' output 3D sia da quello in due dimensioni che la materia si diffonde maggiormente verso il lato in cui i coefficienti di diffusione sono maggiori.

$ fick -x 5 -y 5 -t 4 - -3d test/ciambella.bmp test/grad_simm.bmp

[$t_0$] [$t_4$] [$t_8$]

[$t_{12}$] [$t_{16}$] [$t_{20}$] [$t_{24}$] [$t_{28}$] [$t_{32}$] [$t_{36}$] [$t_{40}$] [$t_{44}$]

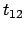
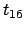
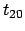
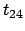
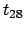
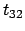
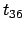
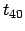
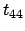
Figura: coefficienti costanti in 3D

[$t_{48}$] [$t_{52}$] [$t_{56}$]

Quì si vede che la concentrazione di materia, all' aumentare di 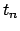$t_n$, non si diffonde in maniera uniforme in tutte le direzioni ma tende a diffondersi con maggiore rapidità nella direzione in cui il coefficiente di diffusione è maggiore.