calculate_b()

La funzione calculate_b() restituisce un vettore; viene chiamata sia se il simulatore lavora in modalità esplicita, sia se lavora in modalità implicita. In modalità esplicita la funzione trova direttamente $C_{n+1}$. Per capire il suo funzionamento si parte dall' equazione (); sommando i termini comuni ed effettuando le sostituzioni $\lambda_x = (\delta T\: D) / {(\delta X)}^2$ e $\lambda_y = (\delta T\: D) / {(\delta Y)}^2$ si ottiene

$$\begin{multline} C_{i,j,n+1} = \lambda_x C_{i+1,j,n} + (1 - 2\lambda_x - 2\lam... ...a_x C_{i-1,j,n} + \lambda_y C_{i,j+1,n} + \lambda_y C_{i,j-1,n}. \end{multline}$$

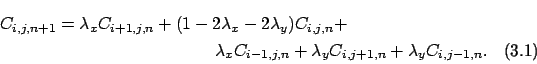
Confrontando il lato destro della () e il lato destro dell' equazione () del metodo implicito si ha che sono uguali a meno di $C_{i,j,n}$. Detto questo risulta semplice unire in una sola funzione il calcolo del lato destro delle due modalità operative. La funzione, lavorando in modalità implicita, restituisce un vettore $b$ dato da $\{2\, Id + D\: B'\} C_n$. Questo sarà il vettore di termini noti del sistema $A\, C_{n+1} = b$.

float *calculate_b(int Dx, int Dy, double Dt,
                   Matrice *D, Matrice *C) {
  int k;
  float *b;

1   if ((b = (float *)malloc(D->r*D->c * sizeof(float))) == NULL)
2     exit(1);

3   for (k = 0; k < (D -> r * D -> c); k++) {

4     b[k] = ((implicit+1) - 2*Lx(k) - 2*Ly(k))* C->m[k];
                                /* (2-2Lx-2Ly)C(k) implicit */
                                /* (1-2Lx-2Ly)C(k) explicit */
5     if ((k-1)%D->c != D->c - 1)
6       b[k] += Lx(k) * C->m[k - 1];          /* LxC(k-1) */

7     if ((k+1)%D->c != 0)
8       b[k] += Lx(k) * C->m[k + 1];          /* LxC(k+1) */

9     if (k - D->c >= 0)
10      b[k] += Ly(k) * C->m[k - D->c];       /* LyC(k-N) */

11    if (k + D->c < D -> r * D -> c)
12      b[k] += Ly(k) * C->m[k + D->c];       /* LyC(k+N) */

13  }
14  return b;
15}

Nelle linee 1-2 si riserva la memoria per il vettore $b$, nel for (linee 3-13) si scrivono gli elementi del vettore. Nella riga 4 è presente la variabile globale implicit che assume il valore $1$ se si sta utilizzando la modalità implicita, 0 altrimenti. Le istruzioni if hanno la stesso scopo di quelle della funzione coefficient_matrix(). La sua complessità è $\Theta(n)$.